Współczynnik Korelacji (CC)
Definicja
Współczynnik Korelacji (CC) to statystyczna miara współzmienności dwóch lub więcej zmiennych. W kontekście tradingu pod pojęciem zmiennej rozumie się akcje, ETFy czy inne instrumenty finansowe. Korelacja pomiędzy dwoma instrumentami finansowymi to nic innego jak stopień, w jakim są one ze sobą związane. Stopień korelacji określa się w skali od -1 do 1. Im współczynnik korelacji bliższy jest wartości 1, tym wyższy stopień korelacji pozytywnej pomiędzy zmiennymi - dane instrumenty będą wspólnie poruszać się w górę bądź w dół. Im współczynnik korelacji bliższy -1, tym bardziej instrumenty te poruszać się będą w przeciwnych kierunkach. Wartość 0 oznacza brak korelacji.
Wysoka korelacja dodatnia
Historia
Współczynnik Korelacji jest stosowany nie tylko w finansach, ale także w analizie statystycznej obejmującej wiele różnych tematów. Stosuje się go od setek lat.
Obliczenia
Przy obliczaniu współczynnika korelacji stosuje się ceny zamknięcia. Poniższe obliczenia dotyczą cen zamknięcia z 12 okresów dla SPY i JPM:
liczby mogą się nieznacznie różnić z powodu zaokrągleń
| OKRES | DATA | INSTRUMENT 1 | INSTRUMENT 2 |
|
|
|
|
| Data | SPY | JPM |
| 1 | 8/1/2013 | 170.66 | 56.54 |
| 2 | 8/2/2013 | 170.95 | 56.40 |
| 3 | 8/5/2013 | 170.70 | 56.10 |
| 4 | 8/6/2013 | 169.73 | 55.49 |
| 5 | 8/7/2013 | 169.18 | 55.30 |
| 6 | 8/8/2013 | 169.80 | 54.83 |
| 7 | 8/9/2013 | 169.31 | 54.52 |
| 8 | 8/12/2013 | 169.11 | 54.09 |
| 9 | 8/13/2013 | 169.61 | 54.29 |
| 10 | 8/14/2013 | 168.74 | 54.15 |
| 11 | 8/15/2013 | 166.38 | 53.29 |
| 12 | 8/16/2013 | 165.83 | 51.83 |
Wszystkie niezbędne dane należy skonfigurować (najlepiej w tabeli), co można wykonać w trzech krokach.
1. Po pierwsze, każdy okres musi zostać podniesiony do kwadratu dla obydwu instrumentów.
| OKRES | DATA | INSTRUMENT 1 | INSTRUMENT 2 | ||
| Data | SPY | JPM | SPY kwadrat | JPM kwadrat | |
| 1 | 8/1/2013 | 170.66 | 56.54 | 29124.84 | 3196.77 |
| 2 | 8/2/2013 | 170.95 | 56.40 | 29223.90 | 3180.96 |
| 3 | 8/5/2013 | 170.70 | 56.10 | 29138.49 | 3147.21 |
| 4 | 8/6/2013 | 169.73 | 55.49 | 28808.27 | 3079.14 |
| 5 | 8/7/2013 | 169.18 | 55.30 | 28621.87 | 3058.09 |
| 6 | 8/8/2013 | 169.80 | 54.83 | 28832.04 | 3006.33 |
| 7 | 8/9/2013 | 169.31 | 54.52 | 28665.88 | 2972.43 |
| 8 | 8/12/2013 | 169.11 | 54.09 | 28598.19 | 2925.73 |
| 9 | 8/13/2013 | 169.61 | 54.29 | 28767.55 | 2947.40 |
| 10 | 8/14/2013 | 168.74 | 54.15 | 28473.19 | 2932.22 |
| 11 | 8/15/2013 | 166.38 | 53.29 | 27682.30 | 2839.82 |
| 12 | 8/16/2013 | 165.83 | 51.83 | 27499.59 | 2686.35 |
2. Dla każdego okresu pomnóż wartość SPY przez odpowiadającą mu wartość JPM. Zwróć uwagę na ostatnią kolumnę.
| OKRES | DATA | INSTRUMENT 1 | INSTRUMENT 2 | |||
| Data | SPY | JPM | SPY kwadrat | JPM kwadrat | SPY x JPM | |
| 1 | 8/1/2013 | 170.66 | 56.54 | 29124.84 | 3196.77 | 9649.12 |
| 2 | 8/2/2013 | 170.95 | 56.40 | 29223.90 | 3180.96 | 9641.58 |
| 3 | 8/5/2013 | 170.70 | 56.10 | 29138.49 | 3147.21 | 9576.27 |
| 4 | 8/6/2013 | 169.73 | 55.49 | 28808.27 | 3079.14 | 9418.32 |
| 5 | 8/7/2013 | 169.18 | 55.30 | 28621.87 | 3058.09 | 9355.65 |
| 6 | 8/8/2013 | 169.80 | 54.83 | 28832.04 | 3006.33 | 9310.13 |
| 7 | 8/9/2013 | 169.31 | 54.52 | 28665.88 | 2972.43 | 9230.78 |
| 8 | 8/12/2013 | 169.11 | 54.09 | 28598.19 | 2925.73 | 9147.16 |
| 9 | 8/13/2013 | 169.61 | 54.29 | 28767.55 | 2947.40 | 9208.13 |
| 10 | 8/14/2013 | 168.74 | 54.15 | 28473.19 | 2932.22 | 9137.27 |
| 11 | 8/15/2013 | 166.38 | 53.29 | 27682.30 | 2839.82 | 8866.39 |
| 12 | 8/16/2013 | 165.83 | 51.83 | 27499.59 | 2686.35 | 8594.97 |
3. Oblicz wartość średnią dla każdej kolumny.
| OKRES | DATA | INSTRUMENT 1 | INSTRUMENT 2 | |||
| Data | SPY | JPM | SPY kwadrat | JPM kwadrat | SPY x JPM | |
| 1 | 8/1/2013 | 170.66 | 56.54 | 29124.84 | 3196.77 | 9649.12 |
| 2 | 8/2/2013 | 170.95 | 56.40 | 29223.90 | 3180.96 | 9641.58 |
| 3 | 8/5/2013 | 170.70 | 56.10 | 29138.49 | 3147.21 | 9576.27 |
| 4 | 8/6/2013 | 169.73 | 55.49 | 28808.27 | 3079.14 | 9418.32 |
| 5 | 8/7/2013 | 169.18 | 55.30 | 28621.87 | 3058.09 | 9355.65 |
| 6 | 8/8/2013 | 169.80 | 54.83 | 28832.04 | 3006.33 | 9310.13 |
| 7 | 8/9/2013 | 169.31 | 54.52 | 28665.88 | 2972.43 | 9230.78 |
| 8 | 8/12/2013 | 169.11 | 54.09 | 28598.19 | 2925.73 | 9147.16 |
| 9 | 8/13/2013 | 169.61 | 54.29 | 28767.55 | 2947.40 | 9208.13 |
| 10 | 8/14/2013 | 168.74 | 54.15 | 28473.19 | 2932.22 | 9137.27 |
| 11 | 8/15/2013 | 166.38 | 53.29 | 27682.30 | 2839.82 | 8866.39 |
| 12 | 8/16/2013 | 165.83 | 51.83 | 27499.59 | 2686.35 | 8594.97 |
| Średnia | 169.1667 | 54.7358 | 28619.6762 | 2997.7049 | 9261.3142 |
Teraz gdy wszystkie dane zostały poprawnie umieszczone w tabeli, można uzupełnić pozostałą część formuły. To zadanie można wykonać w trzech krokach.
- Oblicz wariancję dla obydwu instrumentów. Wariancja = Średnia do kwadratu - (wartość średnia * wartość średnia)
Wariancja SPY: 2.3151
Wariancja JPM: 1.697 - Oblicz kowariancję instrumentów. Kowariancja = (Wartość średnia instrumentu1 x Instrument2) - (Wartość średnia instrumentu1 x Wartość średnia instrumentu2)
Kowariancja SPY & JPM = 1.8395 - Oblicz współczynnik korelacji. Współczynnik Korelacji = Kowariancja / Pierwiastek kwadratowy z (Wariancja instrumentu1 x Wariancja instrumentu2)
Współczynnik Korelacji SPY & JPM = 0.9432
Podstawy
Pomimo tego, że współczynnik korelacji (CC) porusza się w zakresie od 1 do -1, nie jest uważany za oscylator. Wartości wahają się pomiędzy korelacją dodatnią i ujemną, wskazując jak ściśle poruszają się ceny danych instrumentów. Współczynnik korelacji +1 jest doskonałą korelacją dodatnią i oznacza, że ceny poruszają się w idealnej synchronizacji. Współczynnik korelacji o wartości -1 jest doskonałą korelacją ujemną i oznacza, że ceny poruszają się w kierunkach dokładnie przeciwnych. Obydwie te skrajności są rzadkie, a współczynnik korelacji często będzie się wahał gdzieś pomiędzy nimi. Współczynnik korelacji równy 0 to punkt środkowy wskazujący, że obecnie nie ma żadnej korelacji pomiędzy tymi dwoma instrumentami.
Wysoka korelacja negatywna
Na co zwracać uwagę
W przeciwieństwie do wielu wskaźników analizy technicznej współczynnik korelacji jest idealny dla inwestycji długoterminowych. Jeśli inwestor dąży do prawdziwie zdywersyfikowanego portfela, to Współczynnik Korelacji może okazać się dość użyteczny. Może on pomóc określić, czy aktywa w Twoim portfelu są zróżnicowane. Innymi słowy, dzięki posiadaniu instrumentów o niskiej korelacji, można uniknąć powielania niepotrzebnego ryzyka.
Podsumowanie
Jak już wcześniej wspomniano, współczynnik korelacji może być użytecznym narzędziem w tworzeniu zróżnicowanego portfela. Należy jednak zawsze pamiętać o tym, że korelacja między dwoma instrumentami będzie się od czasu do czasu zmieniać. Ten wskaźnik pomoże traderowi dowiedzieć się o takich zmianach i odpowiednio dostosować inwestycje.
Argumenty
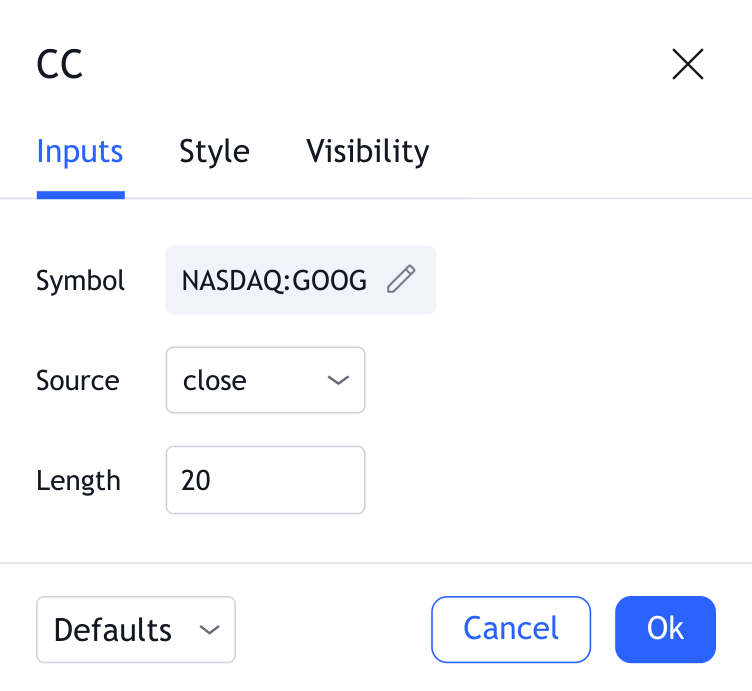
Symbol
Drugi instrument, który zostanie porównany z pierwotnym instrumentem na wykresie.
Długość
Okres czasu, który ma być używany podczas obliczania korelacji. Wartość domyślna to 20 dni.
Źródło
Określa które dane z każdego słupka zostaną użyte do obliczeń. Wartość domyślna to zamknięcie.
Styl

Korelacja
Przełącza widoczność Współczynnika Korelacji, a także widoczność linii cenowej pokazującej rzeczywistą bieżącą cenę Współczynnika Korelacji. Pozwala także wybrać kolor, grubość i typ wizualny Współczynnika Korelacji (wartość domyślna to obszar).
Poziom
Przełącza widoczność i ustawia poziom ceny trzech dodatkowych linii poziomych. Domyślnie linie wyświetlają maksymalną i minimalną możliwą wartość obliczenia współczynnika korelacji (odpowiednio 1 i -1) oraz poziom zerowej korelacji. Możliwe jest również ustawienie koloru, grubości linii i stylu wizualnego każdej linii (domyślnie jest to Linia przerywana).