A better alternative to Fibonacci grid

🙏🏻 Fibonacci based grid is a great inspiration from the Universe, but imo ain’t the final product, and here it is:

For traders
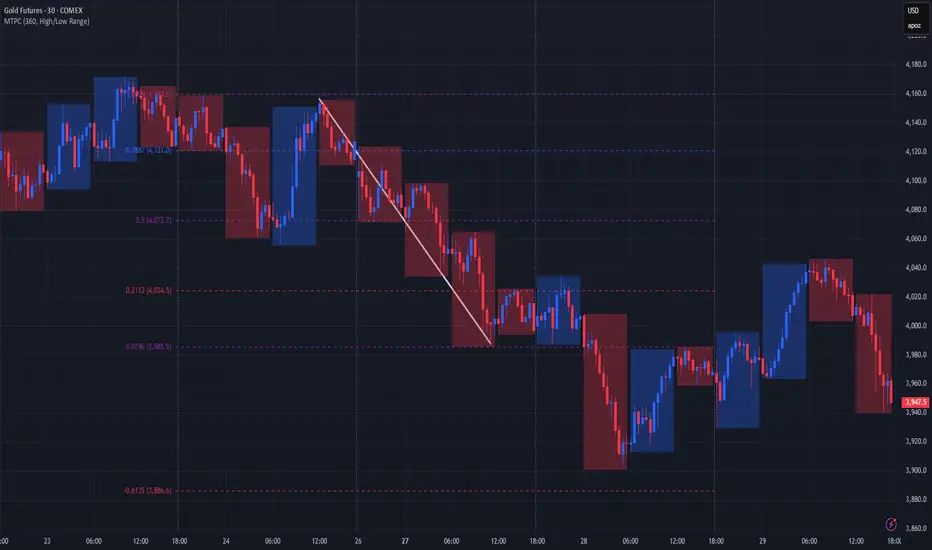
Use these values above and put em into grid tool here, and you’ll end up with uniform distribution based grid:

1.6134612334371357
1.0196152422706632
0.7886751345948129
0.5
0.21132486540518708
-0.019615242270663247
-0.6134612334371357

Then about how to apply it, you can divide trading activity by analytical units, these are in turn are based on:

^^ by price


^^ by time


^^ by signed volume waves/volume delta


Explanation
If you’ve followed my latest work you know I’ve identified a way to combine higher order moments to construct natural data driven estimates of data’s extremums and “ever possible” values (I still got no idea how no1 Ever posted it anywhere over the last centuries).

Now imagine you got only 2 input values: actual max and min (just like in Fibo grid, it ain’t knows nothing else). Given only these 2 values we can model stuff with uniform distribution that has precisely known values of standardized moments, so we end up with (and remember that uniform distro is symmetric around its mid, so all odd moments are zero):

dev   = 1 / math.sqrt(12) //standard deviation
kurt  = 1.8               //kurtosis (not excess ofc, the raw one)
hkurt = 27 / 7            //hyperkurtosis, 6th moment, raw af as well

0.5 + dev * hkurt
0.5 + dev *  kurt
0.5 + dev        
0.5              
0.5 - dev        
0.5 - dev *  kurt
0.5 - dev * hkurt

And the resulting output of it u seen at the beginning of the post, notice how the edges *almost* match your lovely golden ratio.


For wanderers:
Now for the wanderers, creators etc etc etc
We might have a new math constant in our hands.
This can’t be a coincidence that limit levels (the ones at the edges) almost match the golden ratio. What if we find some kind of ‘almost’ uniform distro, where the limit levels would ‘exactly’ match the golden ratio? No problem - Beta distribution with parameters alpha = beta = (smth just a bit greater than 1).

I solved it numerically in python with mpmath library (necessary for high precision stuff, default packages are gonna truncate too much and we work with gamma functions there, high powers, huge numbers).

The following constant used as both parameters for Beta distribution provides us an almost uniform beautiful distro, with a minimal necessary deviation from uniform distro if u pls, just with a lil bit gently smoothed corners, and all connected to fibonacci sequence and golden ratio:

1.013156499304251804283836146883597463164059088989506487984660881392552993230097518061037104047261922219476043198153474114525730243848097530913517155085537693517359999905511951459927003624291626547046737804828112785002512650…

… and it goes on and on. I called it Sagitta constant, because visually it creates that beautiful almost flat shape, the minimal natural curvature. And now if we put this as c in Beta(c, c) following the same levels construction method from before we get these levels:

std = 0.28741741
K   = 1.80628205
Hk  = 3.88993123

0.5 + std * hk  = 1.61803398
0.5 + std * k   = 1.01915692
0.5 + std       = 0.78741741
0.5             = 0.5
0.5 - std       = 0.21258258
0.5 - std * k   = -0.01915692
0.5 - std * hk  = -0.61803398

Visuals, plots, graphics
^^ here you can see how our resulting distro & derivatives look like, kinda cute aye?

Beta(c, c), where c is our constant Sagitta, actually might be a natural prior for Bayesian stuff, almost a boxcar windowing function for DSP so u gonna tame that famous spectral leakage, or a kernel for KDE, like u name it, every case when u need a uniform shape yet with slightly relaxed endpoints, you can use it in design and architecture.

Go for it bros, test it in your R&D. Maybe some1 gonna use it to prove Riemann assumption conjecture, if u get dat milli send me 25% ima find a good use for it.

∞